A. MODEL MATEMATIKA
Ialah suatu cara sederhana untuk memecahkan suatu permasalahan dengan menggunakan persamaan-persamaan atau pertidaksamaan matematika.
Contoh :
1. Kelereng Ali di tambah kelereng Budi lebih banyak dari kelereng Imam. Kelereng Imam sebanyak 5 butir,maka model matematika persamaan tersebut adalah :
Penyelesaiaan :
Misal : kelereng Ali = x
kelereng Budi = y
kelereng Imam = 5
Maka : x + y > 5
2. Harga 1 Kg gula di tambah 2 Kg beras paling tinggi sebesar Rp 1.000,- dan harga 2 Kg gula di tambah 3 Kg beras paling tinggi sebesar Rp 1.500,- Tentukan model matematika pernyataan tersebut.
Penyelesaiaan :
Misal : harga 1 Kg gula = x
harga 1 Kg beras = y
Model matematika dari pernyataan I adalah : x + 2y ≤ 1000
Model matematika dari pernyataan II adalah : 2x + 3y ≤ 1500
B. MENGGUNAKAN MODEL MATEMATIKA
Hal penting yang harus di perhatikan adalah :
1. Jika model matematika berupa persamaan,maka di selesaikan dengan eleminasi atau substitusi.
2. Jika model matematika berupa pertidaksamaan,maka untuk menyelesaikannya harus di tempuh langkah-langkah sebagai berikut :
a. Tentukan persamaan (titik potong dengan sumbu x dan sumbu y)
b. Gambarkan pada silang sumbu kartesius
c. Tentukan daerah yang memenuhi
d. Tentukan titik optimum yang di kehendaki
e. Masukkan koordinat titik optimum pada fungsi sasaran/obyektif
Contoh :
Rokok A yang harganya Rp 800,- per bungkus di jual dengan laba Rp 100,- per bungkus,sedangkan rokok B yang harganya Rp 600,- per bungkus di jual dengan laba Rp 80,- per bungkus. Seorang pedagang rokok mempunyai modal Rp 720.000,- dan kiosnya maksimum dapat menampung 1000 rokok. Berapa bungkus rokok A dan rokok B yang harus di beli pedagang itu agar memperoleh laba sebesar-besarnya.
Penyelesaian :
Model matematika :
Harga : 800x + 600y ≤ 720.000
4x + 3y ≤ 3.600
Kapasitas : x + y ≤ 1000
Laba : 100x + 80y → fungsi sasaran
x ≥ 0 ; y = ≥
Model matematika di atas kita gambarkan ke sistem sumbu kartesius yaitu :
- Cara mencari daerah yang memenuhi :
Misal : x + y ≤ 1000
Coba titik (0,0) → 0 + 0 ≤ 1000
Jika betul berarti (0,0) memenuhi
- Mencari titik E
Titik E = (600,400)
100x + 80y
O (0,0) → 0
A (900,0) → 90.000
E (600,400) → 60.000 + 32.000
D (0,1000) → 80.000
Jadi yang menghasilkan maksimum adalah titik E. Pedagang tersebut akan menghasilkan laba maksimum Rp 92.000,- apabila membeli rokok A 600 bngkus dan rokok B 400 bungkus.











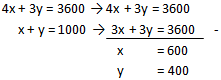




0 komentar:
Posting Komentar