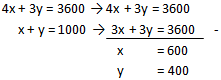Minggu, 17 April 2011
Sabtu, 29 Januari 2011
Matriks
Posted by Indira
On 22.42
Pengertian matriks
· Matriks adalah susunan bilangan dalam suatu perseg i panjang yang diatur berdasarkan baris dan kolom.
· Ordo atau ukuran dari suatu matriks adalah banyak baris dan kolom dari suatu matriks
· Susunan horizontal disebut deng an baris
· Susunan vertical disebut dengan kolom
TRANSPOSE (Baris à Kolom)
Transpose Matriks A adalah sebuah matriks baru yang disusun dengan cara menuliskan baris pertama matriks A menjadi kolom pertama matriks baru, baris kedua matriks A menjadi kolom kedua matriks baru, dan seterusnya. Tra nspose matriks A dinotasikan dengan AT. Jika matriks A berordo m x n, maka AT berordo n x m.
KESAMAAN DUA MATRIKS
Matriks A dan matrik B dikatakan sama (A = B), jika dan hanya jika :
Perkalian Matrik dengan Skalar
Apabila A adalah sebuah matriks berordo m x n dan k adalah suatu bilangan real, maka kA adalah matriks baru berordo m x n yang diperoleh dari hasil perkalian k dengan elemen elemen matriks A
Perkalian Dua Matriks
Matriks A dapat dikalian dengan matriks B jika banyak kolom matriks A sama dengan banyak baris matriks B. Dengan kata lain Apabila A adalah matriks berordo m x n dan matriks B berordo n x p, hasil perkalian matriks A dengan matriks B adalah matriks baru (missal matriks C) yang berordo m x p. Hasil perkalian matriks A dengan matriks B yang sepadan diperoleh dengan cara mengalikan masing masing baris matriks A dengan masing masing kolom matriks B, kemudian menjumlahkannya.
Sifat Perkalian dua Matriks atau lebih yang sepadan
Distributif Kanan : (B + C). A = B. A + C. A
bentuk algoritma
· Matriks adalah susunan bilangan dalam suatu perseg i panjang yang diatur berdasarkan baris dan kolom.
· Ordo atau ukuran dari suatu matriks adalah banyak baris dan kolom dari suatu matriks
· Susunan horizontal disebut deng an baris
· Susunan vertical disebut dengan kolom
TRANSPOSE (Baris à Kolom)
Transpose Matriks A adalah sebuah matriks baru yang disusun dengan cara menuliskan baris pertama matriks A menjadi kolom pertama matriks baru, baris kedua matriks A menjadi kolom kedua matriks baru, dan seterusnya. Tra nspose matriks A dinotasikan dengan AT. Jika matriks A berordo m x n, maka AT berordo n x m.
KESAMAAN DUA MATRIKS
Matriks A dan matrik B dikatakan sama (A = B), jika dan hanya jika :
- Ordo kedua matriks sama
- Semua elemen yang seletak (bersesuaian) mempunyai nilai yang sama
Perkalian Matrik dengan Skalar
Apabila A adalah sebuah matriks berordo m x n dan k adalah suatu bilangan real, maka kA adalah matriks baru berordo m x n yang diperoleh dari hasil perkalian k dengan elemen elemen matriks A
Perkalian Dua Matriks
Matriks A dapat dikalian dengan matriks B jika banyak kolom matriks A sama dengan banyak baris matriks B. Dengan kata lain Apabila A adalah matriks berordo m x n dan matriks B berordo n x p, hasil perkalian matriks A dengan matriks B adalah matriks baru (missal matriks C) yang berordo m x p. Hasil perkalian matriks A dengan matriks B yang sepadan diperoleh dengan cara mengalikan masing masing baris matriks A dengan masing masing kolom matriks B, kemudian menjumlahkannya.
Sifat Perkalian dua Matriks atau lebih yang sepadan
- Perkalian matriks pada umumnya tidak komutatif
- Perkalian matriks bersifat asosiatif
- Perkalian matriks bersifat distributif
Distributif Kanan : (B + C). A = B. A + C. A
- Dalam perkalian matriks yang hanya memuat matriks-matriks persegi dengan ordo yang sama, terdapat sebuah matrik identitas, yaitu matrik satuan I, yang bersifat : I . A = A . I
- Jika A . B = O, belum tentu A = O atau B = O
- Jika p dan q adalah bilangan bilangan real, serta A dan B adalah matrik matriks, maka berlaku hubungan
- Jika At dan Bt berturut-turut adalah transpose dari matriks A dan matriks B maka :
bentuk algoritma
- Deklarasikan variable i untuk iterasi, j untuk iterasi, k untuk iterasi, bar_a untuk jumlah baris pada matriks A, kol_a untuk jumlah kolom pada matriks A, bar_b untuk jumlah baris pada matriks B, kol_b untuk jumlah kolom pada matriks B, mat_a dengan tipe array of integer untuk menampung nilai matriks A, mat_b dengan tipe array of integer untuk menampung nilai matriks B, mat_c dengan tipe array of integer untuk menampung hasil perkalian kedua matriks.
- Masukkan jumlah baris pada matriks A lalu nyatakan ke variable bar_a, jumlah kolom pada matriks A lalu nyatakan ke variable kol_a, jumlah baris pada matriks B lalu nyatakan ke variable bar_b, serta jumlah kolom pada matriks B lalu nyatakan ke variable kol_b.
- Bila nilai pada bar_a tidak sama dengan nilai pada kol_b atau nilai pada kol_a tidak sama dengan nilai pada bar_b maka cetak “Kolom A = Baris B & Baris A = Kolom B!!!” dan kembali ke langkah 2, namun bila tidak maka lakukan langkah 4 s/d 41.
- Cetak “ Nilai matriks A ” untuk membedakan nilai yang akan dimasukkan adalah nilai pada matriks A, bukan nilai pada matriks B.
- Isi variable i dengan 0.
- Selama nilai pada i kurang dari jumlah baris pada matriks A lakukan langkah 7 s/d 11.
- Isi variable j dengan 0.
- Selama j kurang dari jumlah kolom pada matriks A lakukan langkah 9 s/d 10.
- Masukkan nilai matriks pada indeks ke-i ke-j dan nyatakan ke mat_a[i][j].
- Tambahkan nilai pada variable j dengan 1.
- Tambahkan nilai pada variabel i dengan 1.
- Cetak “ Nilai matriks B ” untuk membedakan nilai yang akan dimasukkan adalah nilai pada matriks B, bukan nilai pada matriks A.
- Isi variable j dengan 0.
- Selama nilai pada j kurang dari jumlah baris pada matriks B lakukan langkah 15 s/d 19.
- Isi variable k dengan 0.
- Selama k kurang dari jumlah kolom pada matriks B lakukan langkah 17 s/d 18.
- Masukkan nilai matriks pada indeks ke-j ke-k dan nyatakan ke mat_b[j][k].
- Tambahkan nilai pada variable k dengan 1.
- Tambahkan nilai pada variabel j dengan 1.
- Isi variabel i dengan 0.
- Selama i kurang dari jumlah baris pada matriks A lakukan langkah 22 s/d 30.
- Isi variabel k dengan 0.
- Selama nilai pada k kurang dari jumlah kolom pada matriks B lakukan langkah 24 s/d 29.
- Isi mat_c pada indeks ke-i ke-k dengan 0.
- Isi j dengan 0.
- Selama j kurang dari jumlah baris pada matriks B lakukan langkah 27 s/d 28.
- Tambahkan nilai pada matriks_c indeks ke-i ke-k dengan hasil kali dari nilai pada mat_a pada indeks ke-i ke-j dengan nilai pada mat_b pada indeks ke-j ke-k kemudian nyatakan ke mat_c pada indeks ke-j ke-k.
- Tambahkan nilai pada j dengan 1.
- Tambahkan nilai pada k dengan 1.
- Tambahkan nilai pada i dengan 1
- Isi i dengan 0.
- Selama nilai i kurang dari jumlah baris pada matriks A lakukan langkah 33 s/d 37.
- Isi k dengan 0.
- Selama nilai k kurang dari jumlah kolom pada matriks B lakukan langkah 35 s/d 36.
- Cetak nilai pada mat_c indeks ke-i ke-k.
- Tambahkan nilai pada variabel k dengan 1.
- Tambahkan nilai pada variabel i dengan 1.
- Tanya apakah user masih ingin mengalikan dua buah matriks.
- Bila jawabannya iya, maka kembali ke langkah ke-2.
- Bila jawabannya tidak, maka program dapat langsung diakhiri.
- Namun jika bukan keduanya, tanyalah kembali (kembali ke langkah 38).
Integral
Posted by Indira
On 22.36
ANTI TURUNAN (INTEGRAL TAK TENTU)
Anti turunan (anti pendiferensialan) atau yang biasa kita sebut integral merupakan suatu operasi balikan (invers) dari pendiferensialan (penurunan).
Definisi :
Kita sebut F suatu anti turunan dari f pada selang I jika DF = f pada I – yakni, jika F’(x) = f (x) untuk semua x dalam I. (jika x suatu titik ujung dari I, F’(x) hanya perlu berupa turunan satu sisi).
Misalnya, kita mencari integral dari f(x) = 3x2 pada (-∞,∞).
Ø Maka kita peroleh integral dari f(x) = 3x2 adalah F(x) = x3. Dan hal ini adalah benar, karena turunan dari integral f(x) → F’(x) = f(x) → 3x2 = 3x2.
Ø Akan tetapi untuk F(x) = x3 + 5 juga memenuhi F’(x) = 3x2, berarti ini juga merupakan suatu anti turunan dari f(x) = 3x2.
Ø Hal ini dipertegas oleh grafik yang menunjukkan bahwa F(x) = 3x2 + C dengan C konstanta sebarang adalah suatu integral dari 3x2 pada (-∞,∞).
Ø Pernyataan inipun dipertegas kembali bahwa setiap integral f(x) = 3x2 berbentuk F(x) = x3 + C sesuai Teorema 4.8.B yang berbunyi :
Jika F’(x) = G’(x) untuk semua-x dalam (a, b), maka terdapat konstanta C sedemikian sehingga F(x) = G(x) + C untuk semua x dalam (a, b).
Dari penjelasan di atas, dapat kita simpulkan bahwa jika suatu fungsi f mempunyai suatu integral, maka turunan dari integral itupun akan bernilai sama walaupun ditambahkan dengan suatu konstanta sebarang.
Jadi mengintegralkan (anti penurunan) suatu fungsi f untuk memperoleh suatu fungsi baru f dapat dituliskan :
∫ f(x) dx = F(x) + C
Persamaan itu adalah benar, asalkan F’(x) = f(x) setara dengan dF(x) = f(x) dx. Sehingga rumus di atas dapat juga dituliskan :
∫ dF(x) = F(x) + C
NOTASI UNTUK ANTI TURUNAN
Jika dalam suatu turunan kita gunakan lambang Dx, maka dalam integral pada awalnya digunakan lambang Ax. Misalnya :
Ax (5x4) = x5 + C
Kemudian, terjadi perubahan pemakaian lambang dan itu digunakan sampai sekarang yaitu dengan menggunakan notasi Leibniz. Lambangnya adalah ∫ f(x) dx. Leibniz memakai istilah integral tak-tentu, dengan ∫ disebut tanda integral dan f(x) disebut integran. Misalnya :
∫ 5x4 dx = x5 + C.
Dimana ∫ disebut tanda integral dan 5x4 disebut integran.
Berikut adalah beberapa aturan penulisan lambang integral.
Teorema A
(Aturan Pangkat). Jika r adalah sebarang bilangan rasional kecuali -1, maka
∫ xr dx = (x r + 1 /r + 1) + C
Perhatikan bahwa anti penurunan suatu pangkat dari x, kita perbesar pangkatnya dengan 1 dan membaginya dengan pangkat yang baru (pangkat semula ditambah 1).
Apabila r = 0 sehingga angka atau bentuk apapun apabila pangkatnya nol memberikan hasil 1, dan integralnya adalah ;
∫ 1 dx = x + C
Teorema B
∫ sin x dx = – cos x + C ∫ cos x dx = sin x + C
INTEGRAL TAK-TENTU ADALAH LINEAR
Teorema C
(Kelinearan dari ∫ . . . dx). Andaikan f dan g mempunyai anti turunan (integral tak tentu) dan andaikan k suatu konstanta. Maka :
i. ∫ k f(x) dx = k ∫ f(x) dx ;
ii. ∫ [ f(x) + g(x)] dx = ∫ f(x) dx + ∫ g(x) dx;
iii. ∫ [ f(x) - g(x)] dx = ∫ f(x) dx – ∫ g(x) dx.
Teorema D
Andaikan g suatu fungsi yang dapat didiferensialkan dan r suatu bilangan rasional yang bukan -1. Maka
∫ [g(x)r g’(x) dx = ([g(x)]r+1 /r + 1) + C
Contoh Soal :
Cari anti turunan F(x) + C dari 18x8 – 16x3 + 6x2 – 2x + 5
Penyelesaian :
∫ (18x8 – 16x3 + 6x2 – 2x + 5) dx
= ∫ 18x8 dx – ∫16x3 dx + ∫6x2 dx – ∫2x dx + ∫5 dx
= 18 ∫x8 dx – 16 ∫x3 dx + 6 ∫x2 dx – 2 ∫x dx + 5 ∫1 dx
= 18 ( x9 /9 + C1) – 16 (x4/4 + C2) + 6 (x3/3+C3) – 2 (x2/2 + C4) + 5 (x + C5)
= 2x9 – 4x4 + 2x3 – x2 + 5x + (18C1 – 16C2 + 6C3 – 2C4 + 5C5)
= 2x9 – 4x4 + 2x3 – x2 + 5x + C
5.2 PENGANTAR UNTUK PERSAMAAN DIFERENSIAL
Persamaan diferensial adalah sebarang persamaan yang mencakup turunan (diferensial) yang tidak diketahui fungsinya. Menyelesaikan suatu persamaan diferensial adalah mencari fungsi yang tidak diketahui itu.
Disini kita hanya meninjau kasus yang paling sederhana, yakni persamaan diferensial tingkat satu yang terpisahkan, maksudnya persamaan dalam bentuk turunan pertama dari fungsi yang tidak diketahui itu dan variabelnya terpisahkan, misalnya suku y berada pada satu ruas dari persamaan dan suku x pada ruas yang lainnya.
PEMISAHAN VARIABEL
Contoh persamaan diferensial yaitu dy/dx = 4x3 + x2/ y3.
Didalam contoh tersebut, terlihat bahwa persamaan dalam bentuk turunan pertama (dy/dx bukan d2y/dx2) dan variabelnya bisa dipisahkan yaitu dengan cara :
→ dy/dx = (4x3 + x2 )/ y3 (kedua ruas dikali y3dx)
→ y3dy = (4x3 + x2 ) dx
Disini terlihat bahwa variabel terpisahkan, suku y berada pada ruas kiri dan suku x berada pada ruas kanan.
MASALAH GERAK
Didalam konteks turunan, kita mengenal s(t) yang menyatakan posisi, v(t) menyatakan kecepatan, dan a(t) menyatakan percepatan. Dimana :
Ø v(t) turunan pertama dari s(t) → s’(t) = ds/dt
Ø a(t) turunan pertama dari v(t) → v’(t) = dv/dt atau
turunan kedua dari s(t) → s”(t) = d2s/ dt2
Dan di dalam konteks integral, kita menuju proses kebalikannya. Misalnya apabila a(t) diketahui maka kita akan mancari v(t) dan s(t) dengan menggunakan konsep integral. Dimana :
Ø v integral dari a → v = ∫ a dt
Ø s integral dari v → s = ∫ v dt
Contoh Soal :
1. Selesaikan persamaan diferensial berikut :
dy / dx = 6x5 + 1; kemudian cari penyelesaian bilamana y = 4 di x = 1.
Penyelesaian :
Ø dy / dx = 6x5 + 1
dy = (3x2 + 1) dx
Ø ∫ dy = ∫ (6x5 + 1) dx
y + C1 = x6 + 1 + C2
y = x6 + 1 + C2 – C1
y = x6 + 1 + C
Ø Substitusikan y =4 dan x = 1
4 = 6 + 1 + C
4 = 7 + C
C = -3
Jadi persamaannya menjadi y = x6 +1 – 3 = x6 -2
2. Pada permukaan planet X, percepatan gravitasi adalah -5,28 kaki per detik. Jika sebuah benda dilemparkan ke atas dari suatu ketinggian awal 500 kaki dengan kecepatan 55 kaki per detik, cari kecepatan dan tingginya 3 detik kemudian.
Penyelesaian :
Diket : a = -5,28
v = 55
s = 500
Dit : a. v → t = 3 = . . . ?
b. s → t = 3 = . . .?
Jawab :
Ø a = dv / dt = -5,28
v = ∫ -5,28 dt
v = -5,28t + C
Karena v = 55 pada t = 0 maka C = 55, sehingga :
v = -5,28t + 55
Ø v = ds / dt = -5,28t + 55
s = ∫(-5,28t + 55) dt
s = -2,64 t2 + 55t + C
Karena s = 500 pada t = 0 maka C = 500, sehingga :
s = -2,64 t2 + 55t + 500
Jadi v dan s pada t = 3, yaitu :
Anti turunan (anti pendiferensialan) atau yang biasa kita sebut integral merupakan suatu operasi balikan (invers) dari pendiferensialan (penurunan).
Definisi :
Kita sebut F suatu anti turunan dari f pada selang I jika DF = f pada I – yakni, jika F’(x) = f (x) untuk semua x dalam I. (jika x suatu titik ujung dari I, F’(x) hanya perlu berupa turunan satu sisi).
Misalnya, kita mencari integral dari f(x) = 3x2 pada (-∞,∞).
Ø Maka kita peroleh integral dari f(x) = 3x2 adalah F(x) = x3. Dan hal ini adalah benar, karena turunan dari integral f(x) → F’(x) = f(x) → 3x2 = 3x2.
Ø Akan tetapi untuk F(x) = x3 + 5 juga memenuhi F’(x) = 3x2, berarti ini juga merupakan suatu anti turunan dari f(x) = 3x2.
Ø Hal ini dipertegas oleh grafik yang menunjukkan bahwa F(x) = 3x2 + C dengan C konstanta sebarang adalah suatu integral dari 3x2 pada (-∞,∞).
Ø Pernyataan inipun dipertegas kembali bahwa setiap integral f(x) = 3x2 berbentuk F(x) = x3 + C sesuai Teorema 4.8.B yang berbunyi :
Jika F’(x) = G’(x) untuk semua-x dalam (a, b), maka terdapat konstanta C sedemikian sehingga F(x) = G(x) + C untuk semua x dalam (a, b).
Dari penjelasan di atas, dapat kita simpulkan bahwa jika suatu fungsi f mempunyai suatu integral, maka turunan dari integral itupun akan bernilai sama walaupun ditambahkan dengan suatu konstanta sebarang.
Jadi mengintegralkan (anti penurunan) suatu fungsi f untuk memperoleh suatu fungsi baru f dapat dituliskan :
∫ f(x) dx = F(x) + C
Persamaan itu adalah benar, asalkan F’(x) = f(x) setara dengan dF(x) = f(x) dx. Sehingga rumus di atas dapat juga dituliskan :
∫ dF(x) = F(x) + C
NOTASI UNTUK ANTI TURUNAN
Jika dalam suatu turunan kita gunakan lambang Dx, maka dalam integral pada awalnya digunakan lambang Ax. Misalnya :
Ax (5x4) = x5 + C
Kemudian, terjadi perubahan pemakaian lambang dan itu digunakan sampai sekarang yaitu dengan menggunakan notasi Leibniz. Lambangnya adalah ∫ f(x) dx. Leibniz memakai istilah integral tak-tentu, dengan ∫ disebut tanda integral dan f(x) disebut integran. Misalnya :
∫ 5x4 dx = x5 + C.
Dimana ∫ disebut tanda integral dan 5x4 disebut integran.
Berikut adalah beberapa aturan penulisan lambang integral.
Teorema A
(Aturan Pangkat). Jika r adalah sebarang bilangan rasional kecuali -1, maka
∫ xr dx = (x r + 1 /r + 1) + C
Perhatikan bahwa anti penurunan suatu pangkat dari x, kita perbesar pangkatnya dengan 1 dan membaginya dengan pangkat yang baru (pangkat semula ditambah 1).
Apabila r = 0 sehingga angka atau bentuk apapun apabila pangkatnya nol memberikan hasil 1, dan integralnya adalah ;
∫ 1 dx = x + C
Teorema B
∫ sin x dx = – cos x + C ∫ cos x dx = sin x + C
INTEGRAL TAK-TENTU ADALAH LINEAR
Teorema C
(Kelinearan dari ∫ . . . dx). Andaikan f dan g mempunyai anti turunan (integral tak tentu) dan andaikan k suatu konstanta. Maka :
i. ∫ k f(x) dx = k ∫ f(x) dx ;
ii. ∫ [ f(x) + g(x)] dx = ∫ f(x) dx + ∫ g(x) dx;
iii. ∫ [ f(x) - g(x)] dx = ∫ f(x) dx – ∫ g(x) dx.
Teorema D
Andaikan g suatu fungsi yang dapat didiferensialkan dan r suatu bilangan rasional yang bukan -1. Maka
∫ [g(x)r g’(x) dx = ([g(x)]r+1 /r + 1) + C
Contoh Soal :
Cari anti turunan F(x) + C dari 18x8 – 16x3 + 6x2 – 2x + 5
Penyelesaian :
∫ (18x8 – 16x3 + 6x2 – 2x + 5) dx
= ∫ 18x8 dx – ∫16x3 dx + ∫6x2 dx – ∫2x dx + ∫5 dx
= 18 ∫x8 dx – 16 ∫x3 dx + 6 ∫x2 dx – 2 ∫x dx + 5 ∫1 dx
= 18 ( x9 /9 + C1) – 16 (x4/4 + C2) + 6 (x3/3+C3) – 2 (x2/2 + C4) + 5 (x + C5)
= 2x9 – 4x4 + 2x3 – x2 + 5x + (18C1 – 16C2 + 6C3 – 2C4 + 5C5)
= 2x9 – 4x4 + 2x3 – x2 + 5x + C
5.2 PENGANTAR UNTUK PERSAMAAN DIFERENSIAL
Persamaan diferensial adalah sebarang persamaan yang mencakup turunan (diferensial) yang tidak diketahui fungsinya. Menyelesaikan suatu persamaan diferensial adalah mencari fungsi yang tidak diketahui itu.
Disini kita hanya meninjau kasus yang paling sederhana, yakni persamaan diferensial tingkat satu yang terpisahkan, maksudnya persamaan dalam bentuk turunan pertama dari fungsi yang tidak diketahui itu dan variabelnya terpisahkan, misalnya suku y berada pada satu ruas dari persamaan dan suku x pada ruas yang lainnya.
PEMISAHAN VARIABEL
Contoh persamaan diferensial yaitu dy/dx = 4x3 + x2/ y3.
Didalam contoh tersebut, terlihat bahwa persamaan dalam bentuk turunan pertama (dy/dx bukan d2y/dx2) dan variabelnya bisa dipisahkan yaitu dengan cara :
→ dy/dx = (4x3 + x2 )/ y3 (kedua ruas dikali y3dx)
→ y3dy = (4x3 + x2 ) dx
Disini terlihat bahwa variabel terpisahkan, suku y berada pada ruas kiri dan suku x berada pada ruas kanan.
MASALAH GERAK
Didalam konteks turunan, kita mengenal s(t) yang menyatakan posisi, v(t) menyatakan kecepatan, dan a(t) menyatakan percepatan. Dimana :
Ø v(t) turunan pertama dari s(t) → s’(t) = ds/dt
Ø a(t) turunan pertama dari v(t) → v’(t) = dv/dt atau
turunan kedua dari s(t) → s”(t) = d2s/ dt2
Dan di dalam konteks integral, kita menuju proses kebalikannya. Misalnya apabila a(t) diketahui maka kita akan mancari v(t) dan s(t) dengan menggunakan konsep integral. Dimana :
Ø v integral dari a → v = ∫ a dt
Ø s integral dari v → s = ∫ v dt
Contoh Soal :
1. Selesaikan persamaan diferensial berikut :
dy / dx = 6x5 + 1; kemudian cari penyelesaian bilamana y = 4 di x = 1.
Penyelesaian :
Ø dy / dx = 6x5 + 1
dy = (3x2 + 1) dx
Ø ∫ dy = ∫ (6x5 + 1) dx
y + C1 = x6 + 1 + C2
y = x6 + 1 + C2 – C1
y = x6 + 1 + C
Ø Substitusikan y =4 dan x = 1
4 = 6 + 1 + C
4 = 7 + C
C = -3
Jadi persamaannya menjadi y = x6 +1 – 3 = x6 -2
2. Pada permukaan planet X, percepatan gravitasi adalah -5,28 kaki per detik. Jika sebuah benda dilemparkan ke atas dari suatu ketinggian awal 500 kaki dengan kecepatan 55 kaki per detik, cari kecepatan dan tingginya 3 detik kemudian.
Penyelesaian :
Diket : a = -5,28
v = 55
s = 500
Dit : a. v → t = 3 = . . . ?
b. s → t = 3 = . . .?
Jawab :
Ø a = dv / dt = -5,28
v = ∫ -5,28 dt
v = -5,28t + C
Karena v = 55 pada t = 0 maka C = 55, sehingga :
v = -5,28t + 55
Ø v = ds / dt = -5,28t + 55
s = ∫(-5,28t + 55) dt
s = -2,64 t2 + 55t + C
Karena s = 500 pada t = 0 maka C = 500, sehingga :
s = -2,64 t2 + 55t + 500
Jadi v dan s pada t = 3, yaitu :
- v = -5,28(3) + 55 = -15,84 + 55 = 39,16 kaki per detik.
- s = -2,64 (3)2 + 55(3) + 500 = -23,76 + 165 + 500 = 641,24 kaki.
HIMPUNAN, BILANGAN, DAN OPERASI ALJABAR
Posted by Indira
On 22.33
Himpunan adalah kumpulan benda-benda dan unsur-unsur yang telah didefinisikan dengan jelas dan juga memiliki sifat keterikatan tertentu.
Macam-macam himpunan
1.Himpunan berhingga
himpunan berhingga adalah himpunan yang jumlah anggotanya bisa dihitung.
Contoh :
A = { bilangan prima kurang dari 10}
= {2, 3, 7, 11}
2.Himpunan tak berhingga
Himpunan tak berhingga adalah himpunan yang jumlah anggotanya tidak bisa dihitung atau tidak terbatas.
Contoh :
B = { bilangan asli }
= {1, 2, 3, 4, 5, ...}
Macam-macam himpunan
1.Himpunan berhingga
himpunan berhingga adalah himpunan yang jumlah anggotanya bisa dihitung.
Contoh :
A = { bilangan prima kurang dari 10}
= {2, 3, 7, 11}
2.Himpunan tak berhingga
Himpunan tak berhingga adalah himpunan yang jumlah anggotanya tidak bisa dihitung atau tidak terbatas.
Contoh :
B = { bilangan asli }
= {1, 2, 3, 4, 5, ...}
Aljabar
Posted by Indira
On 22.32
Aljabar (Algebra) adalah cabang matematika yang mempelajari struktur, hubungan dan kuantitas. Untuk mempelajari hal-hal ini dalam aljabar digunakan simbol (biasanya berupa huruf) untuk merepresentasikan bilangan secara umum sebagai sarana penyederhanaan dan alat bantu memecahkan masalah. Contohnya, x mewakili bilangan yang diketahui dan y bilangan yang ingin diketahui. Sehingga bila Andi mempunyai x buku dan kemudian Budi mempunyai 3 buku lebih banyak daripada Andi, maka dalam aljabar, buku Budi dapat ditulis sebagai y = x + 3. Dengan menggunakan aljabar, Anda dapat menyelidiki pola aturan aturan bilangan umumnya. Aljabar dapat diasumsikan dengan cara memandang benda dari atas, sehingga kita dapat menemukan pola umumnya.
Aljabar telah digunakan matematikawan sejak beberapa ribu tahun yang lalu. Sejarah mencatat penggunaan aljabar telah dilakukan bangsa Mesopotamia pada 3.500 tahun yang lalu. Nama Aljabar berasal dari kitab yang ditulis pada tahun 830 oleh Matematikawan Persia Muhammad ibn Musa al-Kwarizmi dengan judul ‘Al-Kitab al-Jabr wa-l-Muqabala’ (yang berarti "The Compendious Book on Calculation by Completion and Balancing"), yang menerapkan operasi simbolik untuk mencari solusi secara sistematik terhadap persamaan linier dan kuadratik. Salah satu muridnya, Omar Khayyam menerjemahkan hasil karya Al-Khwarizmi ke bahasa Eropa. Beberapa abad yang lalu, ilmuwan dan matematikawan Inggris, Isaac Newton (1642-17 27) menunjukkan, kelakuan sesuatu di alam dapat dijelaskan dengan aturan atau rumus matematika yang melibatkan aljabar, yang dikenal sebagai Rumus Gravitasi Newton.
Aljabar bersama-sama dengan Geometri, Analisis dan Teori Bilangan adalah cabang-cabang utama dalam Matematika. Aljabar Elementer merupakan bagian dari kurikulun dalam sekolah menengah dan menyediakan landasan bagi ide-ide dasar untuk Ajabar secara keseluruhan, meliputi sifat-sifat penambahan dan perkalian bilangan, konsep variabel, definisi polinom, faktorisasi dan menentukan akar pangkat.
Sekarang ini istilah Aljabar mempunyai makna lebih luas daripada sekedar Aljabar Elementer, yaitu meliputi Ajabar Abstrak, Aljabar Linier dan sebagainya. Seperti dijelaskan di atas dalam aljabar, kita tidak bekerja secara langsung dengan bilangan melainkan bekerja dengan menggunakan simbol, variabel dan elemen-elemen himpunan. Sebagai contoh Penambahan dan Perkalian dipandang sebagai operasi secara umum dan definisi ini menuju pada struktur bilangan seperti Grup, Ring, dan Medan (fields).
Asal Mula Aljabar
Asal mula Aljabar dapat ditelusuri berasal dari bangsa Babilonia Kuno yang mengembangkan sistem aritmatika yang cukup rumit, dengan hal ini mereka mampu menghitung dalam cara yang mirip dengan aljabar sekarang ini. Dengan menggunakan sistem ini, mereka mampu mengaplikasikan rumus dan menghitung solusi untuk nilai yang tak diketahui untuk kelas masalah yang biasanya dipecahkan dengan menggunakan persamaan Linier, Persamaan Kuadrat dan Persamaan Linier tak tentu. Sebaliknya, bangsa Mesir, dan kebanyakan bangsa India, Yunani, serta Cina dalam milenium pertama sebelum masehi, biasanya masih menggunakan metode geometri untuk memecahkan persamaan seperti ini, misalnya seperti yang disebutkan dalam ‘the Rhind Mathematical Papyrus’, ‘Sulba Sutras’, ‘Euclid's Elements’, dan ‘The Nine Chapters on the Mathematical Art’. Hasil karya bangsa Yunani dalam Geometri, yang tertulis dalam kitab Elemen, menyediakan kerangka berpikir untuk menggeneralisasi formula matematika di luar solusi khusus dari suatu permasalahan tertentu ke dalam sistem yang lebih umum untuk menyatakan dan memecahkan persamaan, yaitu kerangka berpikir logika Deduksi.
Seperti telah disinggung di atas istilah ‘Aljabar’ berasal dari kata arab "al-jabr" yang berasal dari kitab ‘Al-Kitab al-Jabr wa-l-Muqabala’ (yang berarti "The Compendious Book on Calculation by Completion and Balancing"), yang ditulis oleh Matematikawan Persia Muhammad ibn Musa al-Kwarizmi. Kata ‘Al-Jabr’ sendiri sebenarnya berarti penggabungan (reunion). Matematikawan Yunani di jaman Hellenisme, Diophantus, secara tradisional dikenal sebagai ‘Bapak Aljabar’, walaupun sampai sekarang masih diperdebatkan siapa sebenarnya yang berhak atas sebutan tersebut Al-Khwarizmi atau Diophantus?. Mereka yang mendukung Al-Khwarizmi menunjukkan fakta bahwa hasil karyanya pada prinsip reduksi masih digunakan sampai sekarang ini dan ia juga memberikan penjelasan yang rinci mengenai pemecahan persamaan kuadratik. Sedangkan mereka yang mendukung Diophantus menunjukkan Aljabar ditemukan dalam Al-Jabr adalah masih sangat elementer dibandingkan Aljabar yang ditemukan dalam ‘Arithmetica’, karya Diophantus. Matematikawan Persia yang lain, Omar Khayyam, membangun Aljabar Geometri dan menemukan bentuk umum geometri dari persamaan kubik. Matematikawan India Mahavira dan Bhaskara, serta Matematikawan Cina, Zhu Shijie, berhasil memecahkan berbagai macam persamaan kubik, kuartik, kuintik dan polinom tingkat tinggi lainnya.
Peristiwa lain yang penting adalah perkembangan lebih lanjut dari aljabar, terjadi pada pertengahan abad ke-16. Ide tentang determinan yang dikembangkan oleh Matematikawan Jepang Kowa Seki di abad 17, diikuti oleh Gottfried Leibniz sepuluh tahun kemudian, dengan tujuan untuk memecahkan Sistem Persamaan Linier secara simultan dengan menggunakan Matriks. Gabriel Cramer juga menyumbangkan hasil karyanya tentang Matriks dan Determinan di abad ke-18. Aljabar Abstrak dikembangkan pada abad ke-19, mula-mula berfokus pada teori Galois dan pada masalah keterkonstruksian (constructibility)
Tahap-tahap perkembangan Aljabar simbolik secara garis besar adalah sebagai berikut:
- Aljabar Retorik (Rhetorical algebra), yang dikembangkan oleh bangsa Babilonia dan masih mendominasi sampai dengan abad ke-16;
- Aljabar yang dikontruksi secara Geometri, yang dikembangkan oleh Matematikawan Vedic India dan Yunani Kuno;
- Syncopated algebra, yang dikembangkan oleh Diophantus dan dalam ‘the Bakhshali Manuscript’; dan
- Aljabar simbolik (Symbolic algebra), yang titik puncaknya adalah pada karya Leibniz.
Klasifikasi dari Aljabar
Aljabar secara garis besar dapat dibagi dalam kategori berikut ini:
1. Aljabar Elementer, yang mempelajari sifat-sifat operasi pada bilangan riil direkam dalam simbol sebagai konstanta dan variabel, dan Aturan yang membangun ekspresi dan persamaan Matematika yang melibatkan simbol-simbol.(bidang ini juga mencakup materi yang biasanya diajarkan di sekolah menengah yaitu ‘Intermediate Algebra’ dan ‘college algebra’);
2. Aljabar Abstrak, kadang-kadang disebut Aljabar Modern, yang mempelajari Struktur Aljabar semacam Grup, Ring dan Medan (fields) yang didefinisikan dan diajarkan secara aksiomatis;
3. Aljabar Linier, yang mempelajari sifat-sifat khusus dari Ruang Vektor (termasuk Matriks);
4. Aljabar Universal, yang mempelajari sifat-sifat bersama dari semua Struktur aljabar.
Dalam studi Aljabar lanjut, sistem aljabar aksiomatis semacam Grup, Ring, Medan dan Aljabar di atas sebuah Medan (algebras over a field) dipelajari bersama dengan telaah Struktur Geometri Natural yang kompatibel dengan Struktur Aljabar tersebut dalam bidang Topologi.
Aljabar Elementer
Aljabar Elementer adalah bentuk paling dasar dari Aljabar, yang diajarkan pada siswa yang belum mempunyai pengetahuan Matematika apapun selain daripada Aritmatika Dasar. Meskipun seperti dalam Aritmatika, di mana bilangan dan operasi Aritmatika (seperti +, −, ×, ÷) muncul juga dalam Aljabar, tetapi disini bilangan seringkali hanya dinotasikan dengan simbol (seperti a, x, y). Hal ini sangat penting sebab: Hal ini mengijinkan kita menurunkan rumus umum dari aturan Aritmatika (seperti a + b = b + a untuk semua a dan b), dan selanjutnya merupakan langkah pertama untuk penelusuran yang sistematik terhadap sifat-sifat sistem bilangan riil.
Dengan menggunakan simbol, alih-alih menggunakan bilangan secara langsung, mengijinkan kita untuk membangun persamaan matematika yang mengandung variabel yang tidak diketahui (sebagai contoh “Carilah bilangan x yang memenuhi persamaan 3x + 1 = 10"). Hal ini juga mengijinkan kita untuk membuat relasi fungsional dari rumus-rumus matematika tersebut (sebagai contoh "Jika anda menjual x tiket, dan kemudian anda mendapat untung 3x - 10 rupiah, dapat dituliskan sebagai f(x) = 3x - 10, dimana f adalah fungsi, dan x adalah bilangan dimana fungsi f bekerja.").
PROGRAM LINIER
Posted by Indira
On 22.28
A. MODEL MATEMATIKA
Ialah suatu cara sederhana untuk memecahkan suatu permasalahan dengan menggunakan persamaan-persamaan atau pertidaksamaan matematika.
Contoh :
1. Kelereng Ali di tambah kelereng Budi lebih banyak dari kelereng Imam. Kelereng Imam sebanyak 5 butir,maka model matematika persamaan tersebut adalah :
Penyelesaiaan :
Misal : kelereng Ali = x
kelereng Budi = y
kelereng Imam = 5
Maka : x + y > 5
2. Harga 1 Kg gula di tambah 2 Kg beras paling tinggi sebesar Rp 1.000,- dan harga 2 Kg gula di tambah 3 Kg beras paling tinggi sebesar Rp 1.500,- Tentukan model matematika pernyataan tersebut.
Penyelesaiaan :
Misal : harga 1 Kg gula = x
harga 1 Kg beras = y
Model matematika dari pernyataan I adalah : x + 2y ≤ 1000
Model matematika dari pernyataan II adalah : 2x + 3y ≤ 1500
B. MENGGUNAKAN MODEL MATEMATIKA
Hal penting yang harus di perhatikan adalah :
1. Jika model matematika berupa persamaan,maka di selesaikan dengan eleminasi atau substitusi.
2. Jika model matematika berupa pertidaksamaan,maka untuk menyelesaikannya harus di tempuh langkah-langkah sebagai berikut :
a. Tentukan persamaan (titik potong dengan sumbu x dan sumbu y)
b. Gambarkan pada silang sumbu kartesius
c. Tentukan daerah yang memenuhi
d. Tentukan titik optimum yang di kehendaki
e. Masukkan koordinat titik optimum pada fungsi sasaran/obyektif
Contoh :
Rokok A yang harganya Rp 800,- per bungkus di jual dengan laba Rp 100,- per bungkus,sedangkan rokok B yang harganya Rp 600,- per bungkus di jual dengan laba Rp 80,- per bungkus. Seorang pedagang rokok mempunyai modal Rp 720.000,- dan kiosnya maksimum dapat menampung 1000 rokok. Berapa bungkus rokok A dan rokok B yang harus di beli pedagang itu agar memperoleh laba sebesar-besarnya.
Penyelesaian :
Model matematika :
Harga : 800x + 600y ≤ 720.000
4x + 3y ≤ 3.600
Kapasitas : x + y ≤ 1000
Laba : 100x + 80y → fungsi sasaran
x ≥ 0 ; y = ≥
Model matematika di atas kita gambarkan ke sistem sumbu kartesius yaitu :
- Cara mencari daerah yang memenuhi :
Misal : x + y ≤ 1000
Coba titik (0,0) → 0 + 0 ≤ 1000
Jika betul berarti (0,0) memenuhi
- Mencari titik E
Titik E = (600,400)
100x + 80y
O (0,0) → 0
A (900,0) → 90.000
E (600,400) → 60.000 + 32.000
D (0,1000) → 80.000
Jadi yang menghasilkan maksimum adalah titik E. Pedagang tersebut akan menghasilkan laba maksimum Rp 92.000,- apabila membeli rokok A 600 bngkus dan rokok B 400 bungkus.